Pre-Calculus Worksheet

Teacher/User Name: DEMO	Name:__________________________
Practice Problems By Easy Worksheet	Period: ________ Date: ____________

Worksheet generated by https://www.easyworksheet.com
All rights reserved. Copyright 1998 Triple Threat Inc.

Solve:

Let f(x) be an increasing function.
The table gives values of f(x) for selected values of x.

x	-3	-5	-7	-9	-11	-13	-15
f(x)	3	4	5	6	7	8	9

The function h is given by

	− 13x² − 5x + 10
h(x) =
	− 12x + 8

(A)(i) The function m is defined by m(x) = hof(x) = h(f(x)). Find the value of m(-7) as a decimal approximation or indicate that it is not defined.

(ii) Find the value of f ^-1(4), or indicate that it is not defined.

(B) (i) Find all values of x, as decimal approximations, for which h(x) = 0, or indicate that there are no such values.

(ii) Determine the end behavior of h as x decreases without bound. Express your answer using the mathematical notation of a limit.

(C) (i) Use the table of values of f(x) to determine if f is best modeled by a linear, quadratic, exponential, or logarithmic function.

(C) (i) Give a reason for your answer based upon the relationship between the change in output values of f and the change in the input values of f.

The price of CDs increases over time. In 1993, Zachary's CDs cost $5, and in 1996, the same CDs cost $6. The price of CDs can be modeled by a function P(t) = a(b)^t where P(t) is the price of CDs and t is the number of years since 1990.

(A) (i) Use the given data to write two equations that can be used to find the values for constants a and b in the expression for P(t).

(ii) Find the values for a and b as decimal approximations.

(B) (i) Use the given data to find the average rate of change of price of CDs, in dollars per year since 1990 from t = 3 to t = 6 years since 1990. Express your answer as a decimal approximation. Show the computations that lead to your answer.

(ii) Consider the average rates of change of P from t = 6 to t = p years since 1990, where p > 7. Are these average rates of change less than or greater than the average rate of change from t = 3 to t = 6 years since 1990 found in (i)? Explain your reasoning.

(iii) Use the average rate of change found in (i) to estimate the price of CDs in 1995. Show the work that leads to your answer.

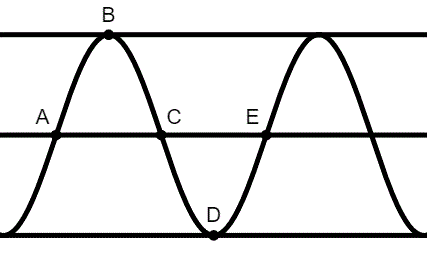
Temperature in a certain city over a year can be modeled by a sinusoidal function.Let t equal the number of days starting with January 1st. The temperature was at a minimum of 44°F at t = 2 days, The temperature was at a maximum of 80°F at t = 185 days.

The siusoidal function f models the temperature, in degrees, as a function of time t, in days since the new year..

(A) The graph of f and its dashed midline for 2 full cycles is shown. Five points, A, B, C, D, and E are labeled on the graph. No scale is indicated, and no axes are presented.

Determine possible coordinates (t, f(t)) for the five points: A, B, C, D, and E.

(B)The function f can be written in the form f(t) = acos(b(t + c)) + d. Find the values of the constants a, b, c, and d.

(i) On the interval (t₁, t₂), which of the following is true about f?

a. f is positive and increasing.

b. f is positive and decreasing.

c. f is negative and increasing.

d. f is negative and decreasing.

(ii) Describe how the rate of change of f is changing on the interval (t₁, t₂).

Directions:
Unless otherwise specified, the domain of a function f is assumed to be the set of real numbers x,
for which f(x) is a real number. Angle measures for trigonometric functions are assumed to be in
radians.
Solutions to equations must be real numbers. Determine the exact value of any expression that can be
obtained without a calculator. For example, log₂8, cos (
π

2
), and sin^-1(1) can be evaluated without a
calculator.
Unless otherwise specified, combine terms using algebraic methods and rules for exponents and
logarithms, where applicable. For example, 2x + 3x, 5² · 5³,
x⁵

x²
, and ln 3 + ln 5 should be rewritten in
equivalent forms.
For each part of the question, show the work that leads to your answers.

(A) The functions k and v are given by:

k(x) = cos²(x) - sin(x)csc(x)
v(x) =
√(5)(25^{3x + 8})

5^{2x − 13}

(i) Rewrite k(x) involving sin(x) and no other trigonometric functions.

(ii) Rewrite v(x) as a single expression of the form 5^{(ax + b)}, where a and b are constants.

(B) The functions j and n are given by:

j(x) = 16^x
n(x) = sec(3πx - ^3π/₄ )

(i) Solve j(x) = 8 for values of x in the domain of j.

(ii) Solve n(x) = -1 for values of x in the interval [¹/₄ , ¹¹/₁₂ ).

f(x) = 2log_₂ (x + 16) - log_₂ (3x² + 49x + 16)

Find all values in the domain of f(x) that yeild an output value of 4.