|
EasyWorksheet's Online Book/Reference Guide Example:
Finding Summations of Arithmetic Series
First, remember that ARITHMETIC means ADDITION, and SERIES is a SUM of a list of numbers. The SUMMATION sign, , is sigma from the Greek Alphabet. Anytime you see
New Vocabulary
What does it mean?
Whenever you are faced with a summation sign, there are numbers on the bottom and top of it like so:| 5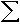 n=-3 | 3n - 2 |
The value on the bottom is where we start. So we'll start at n = -3. And we end up at the value on the top. So we'll end at n = 5. The function is written in the middle. It really doesn't matter what type of function you have!
In order to solve this problem, we'll make a chart. One column of the chart will be n (our variable) and the other side will be 3n - 2 (the function). We simply fill in our n values to 3n - 2 in order to get the other value. For instance, we can plug in -1 for n. Hence, 3n - 2 = 3(-1) - 2 = -3 - 2 = -5. Notice that when n = -1, we have -5 under 3n - 2.
n 3n - 2 ----------- -3 -11 -2 -8 -1 -5 ← See the -5 here? 0 -2 1 1 2 4 3 7 4 10 5 13
Finally, we SUM up all the numbers on the right:
-11 + -8 + -5 + -2 + 1 + 4 + 7 + 10 + 13 = 9.
This is too much work!
Well.. There is a formula!
What happens when we add -11 + 13? (we get 2)
-11 + -8 + -5 + -2 + 1 + 4 + 7 + 10 + 13
\____________________________________/
And what about -8 + 10? (2)
-11 + -8 + -5 + -2 + 1 + 4 + 7 + 10 + 13
\_________________________/
And -5 and 7? (2) (see a pattern yet?)
-11 + -8 + -5 + -2 + 1 + 4 + 7 + 10 + 13
\________________/
How about -2 and 4?
-11 + -8 + -5 + -2 + 1 + 4 + 7 + 10 + 13
\_______/
Then notice that 1 and 1 (pairing 1 with itself) gives 2 as well?
Since there are 9 values total, the total number of groupings is 4 1/2 = 9/2 = the number of values divided by 2!
And we know that the sum is 9/2(-11 + 13)
In other words, the sum of the first n terms is:
Sn = n/2(first term + last term)
Example #1
| 3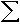 n=0 | 5 - 2(n-1) = |
n 5 - 2(n-1) ------------------- 0 7 1 5 2 3 3 1Then we'll add: 7 + 5 + 3 + 1 = 16 ← our answer!
Example #2
| 229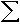 n=-30 | 2n + 5 = |
In this case, it would be easier to use the formula. So we'll begin by finding the first and last terms:
The first term (filling in n = -30) :
2(-30) + 5 = -60 + 5 = -55
The last term (filling in n = 229) :
2(229) + 5 = 458 + 5 = 463
Next, subtract the upper and lower bounds and add 1 to get the number of terms:
(229) - (-30) + 1 = 229 + 30 + 1 = 260.
Now, we'll fill in the formula:
Sn = n/2(first term + last term)
Sn = (260)/2(-55 + 463) = (130)(408) = 53040
Aren't you glad we used the formula? I wouldn't want to make a chart with 260 entries!! (Warning: Only use the formula in the case of ARITHMETIC sequences!! )
Test Taking Strategies
For multiple choice tests, the best thing you can do is remember that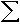 means SUM. That way no matter what function you are given, you can always find the sum in a chart!
Review What You Learned
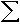means SUM!
The formula for summing an ARITHMETIC sequence (linear function) is
Sn = n/2(first term + last term)